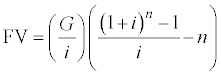
Go to the Prior Tip "Creativity in OR/MS:
Creativity-Enhancing Strategies"
Skipping obsolete Tip 15
Go to the Next Tip"Shareholders Aren't Everything"
Return to MaxValue Home Page
While studying for the Certified Cost Engineer exam, I can across an interesting formula. You might find it useful for discounted cash-flow analysis.
Suppose that you forecast a cost or some other cashflow element to increase linearly. The annual cash flows are G, 2G, 3G, and so forth. The "gradient formula" calculates the future value of periodic, incremental component.
A gradient is a linearly-increasing cashflow. A fairly simple equation expresses the future value. The cash-flow model assumed is:
| Time, t, in years |
0 | 1 | 2 | 3 | 4 | 5 |
| CF | 0 | 0 | G | 2G | 3G | 4G |
The future value for the gradient stream for t=0 to n years is:
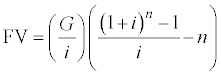
or, as a line formula,
FV=(G/i)*(((1+i)^n-1)/i-n).
where
| G |
is the periodic payment increase (gradient) amount. The first cashflow (CF) of $0 amount occurs at at time t=1, $G at t=2, $2G at t=3, ... | |
| i | is the compounding interest rate per year (corresponds to the present value (PV) discount rate) | |
| n | is the number of years until the final payment. |
If the present value (rather than future value) is needed, adjust by: PV = FV(1+i)-t = FV(1+i)^-t. Further, one might want to translate the cashflow forward 6 or 18 months for mid-period discounting.
--John Schuyler, December 1996 (rev. 10-Aug-99)